گروه ریاضی
.................// گروه ریاضی ، فیزیک و رایانه مدارس جمهوری اسلامی ایران - در لبنان ، سوریه و اردن // .................. سرگروه آموزشی : محمدرضا حکیمیانگروه ریاضی
.................// گروه ریاضی ، فیزیک و رایانه مدارس جمهوری اسلامی ایران - در لبنان ، سوریه و اردن // .................. سرگروه آموزشی : محمدرضا حکیمیاننمونه سوال حل شده از استقرای ریاضی تعمیم یافته
نشان دهید عدد طبیعی مناسبی مانند m وجود دارد که برای هر عدد طبیعی n بزرگتر یا مساوی m داریـم: 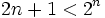
پاسخ: با قرار دادن مقادیر طبیعی برای m متوجه می شویم که m مناسب 3 است چرا که برای اولین بار حکم برای m=3 درست است. حال نشان میدهیم حکم برای هر عدد طبیعی 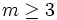 برقرار است.
برقرار است.
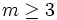 برقرار است.
برقرار است. 1- 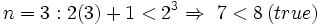
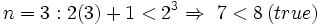
2- اکنون در این مرحله فرض (فرض استقرا) می کنیم نامساوی فوق برای هر عدد طبیعی  درست باشد یعنی:
درست باشد یعنی:
 درست باشد یعنی:
درست باشد یعنی: 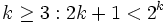
3- نشان میدهیم حکم داده شده برای (n=k+1 ،(k>2 درست است، یعنی:
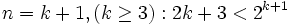 (حکم استقرا)
(حکم استقرا) برای این منظور از فرض استقرا استفاده کرده و به طرفین فرض عدد 2 را اضافه می کنیم، داریم:

حال با مقایسه نامساوی اخیر و حکم استقرا کافی است نشان دهیم:
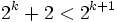
برای این کار از اثبات بازگشتی کمک میگیریم:
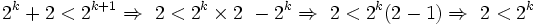
مشاهده می شود نامساوی 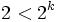 برای K>2 همواره درست است و چون تمامی روابط برگشت پذیرند، لذا
برای K>2 همواره درست است و چون تمامی روابط برگشت پذیرند، لذا 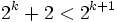 برقرار بوده و به این ترتیب حکم برای هر عدد طبیعی
برقرار بوده و به این ترتیب حکم برای هر عدد طبیعی 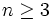 برقرار است.
برقرار است.
برای نمایش آواتار خود در این وبلاگ در سایت Gravatar.com ثبت نام کنید. (راهنما)






















































ایمیل شما بعد از ثبت نمایش داده نخواهد شد